Today we'll deal with another element that is essential to sound synthesis: Filters. They are widely used in subtractive synthesis, which is the most widespread form of synthesis, making filters pretty common on a great number of hardware and virtual instruments.
We’ll come back to subtractive synthesis later. But I can tell you already that the idea behind it is to shape sound starting with a signal that is rich in harmonics, which you can remove or highlight…thanks to filters!
There are different types of filters, depending on the frequency range you want to cut or boost: Low-pass filters, high-pass filters, band-pass filters, and notch filters.
Before analyzing their differences, let’s first take look at their similarities.
Common characteristics
All filters work by the combination of one or more “cut-off” frequencies and a “slope.”
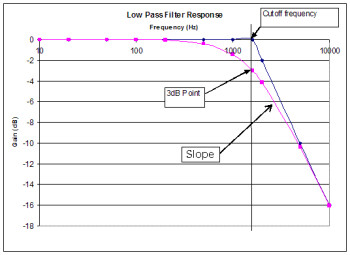
The cut-off frequency is a frequency defined by the user of the filter, usually with a potentiometer. It is from this frequency ─ or sometimes right below it, depending on the filter ─ that the other frequencies are cut (although “attenuated” would be a more correct description).
The slope of the filter determines how severe the process will be.
The attenuation that takes place is expressed in decibels/octave. The more decibels, the more drastic the attenuation. Thus, the boost produced by a filter with a 12db/octave slope will be twice as high as that produced by a filter with a 6db/octave slope.
You will often see on synths an indication regarding the number of “poles” the filter has: 2-pole, 3-pole, etc. This is just a way of defining the slope of the filter in 6db/octave steps. So, a 2-pole filter refers to a filter with a 12dB/octave slope, while a 3-pole filter has a 18dB/octave slope and so on.
The standard reference in terms of filters is still the 4-pole Moog (24db/octave), which is one of the most severe and “typical” filters on the market.
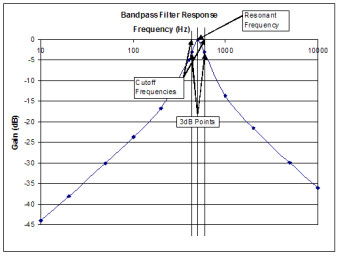
Do note that the cut-off frequency of the filter can be emphasized by a parameter that is almost always present on every filter: Resonance (for an example, see the “Band-pass Filter” section).
Now that the similarities are clear, we can move on to the differences between these filters.
Low-pass filter
This is the most common type of filter in synthesis, to the extent that some units offer only this type of filtering. It is conceived to leave intact the frequencies below the cut-off frequency and attenuate all other frequencies above it.
It also called a high-cut filter sometimes.
Here’s an audio example with a signal processed with a low-pass where we shift the cut-off frequency downwards and then upwards again:
And here’s the same example with the resonance effect:

High-pass filter
It’s the opposite to the previous one. The high-pass filter is conceived to leave intact the frequencies above the cut-off frequency and attenuate all other frequencies below it.
It also called a low-cut filter sometimes.
Here’s an audio example with a signal processed with a high-pass where we shift the cut-off frequency upwards and then downwards again:

Band-pass filter
This kind of filter is conceived to only let through a given frequency range between two limits. Unlike the two precedent filters, this filter has two cut-off frequencies, which correspond to the lower and a higher limits. So this filter is the combination of a high-pass and a low-pass filter.
This is the type of filter used in radio and TV to allow you to switch channels or radio stations by limiting the broadcast frequency range (not to be confused with the audio frequencies) of each channel or station.
Here’s an audio example with a signal processed with a band-pass where we shift the cut-off frequencies upwards and then downwards again:

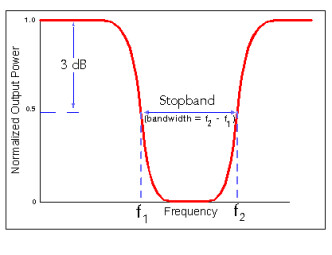
Band-stop (or Notch) filter
This last type of filter is the opposite of the previous one: It defines a frequency range between two limits to be attenuated.
This filter also has two cut-off frequencies and, thus, also combines a high-pass and a low-pass.