In this final installment regarding speaker specs, I'll address distortion. It's interesting to understand why it's a spec that's seldom specified by speaker manufacturers, unlike with amps, which always include it.
Distortion on its own terms
The basic principle of a sound reproduction system is to reproduce an audio signal as faithfully as possible, avoiding any signal degradation. In this case, we’re not talking about distortion as a deliberate effect. Distortion appears when the output signal is altered with regard to the input one (not considering the overall increase in volume). There are several types of distortion, depending on the effects they produce: Linear distortion and non-linear distortion (each of them with its own sub-categories).
Linear distortion: frequency and phase response
Linear distortion includes alterations in terms of frequency response and phase. If the amplitude of all frequencies isn’t rendered with the same accuracy and the response time isn’t the same for all frequency bands, then the signal is considered to be distorted. This type of distortion is called “linear” because it doesn’t generate any new frequencies, i.e. the frequencies at the output are the same as the ones at the input, you only need to consider the differences in amplitude and phase.
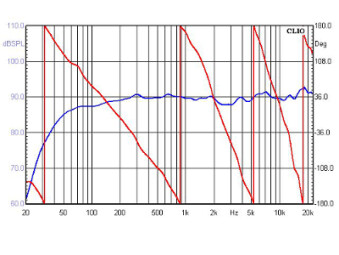
Frequency and phase response are plotted in curves. An ideal response means that there are no differences between source and output, and the latency is the same for the entire frequency range reproduced (phase doesn’t depend on frequency). At least that’s what the theoretical model says, but it’s hardly achievable, especially if you want to cover the entire hearing range. Lots of parameters come under consideration. Speakers, enclosures and filters are complex products and each of them contributes, in its own way, to create a bit of distortion.
Graph taken from a hi-fi speaker depicting the frequency (blue) and phase (red) response curves. The dB SPL reading on the left is meant to help you read the frequency response. The angle (in degrees), to the right, corresponds to the phase response. At the bottom is the frequency in Hertz.
Non-linear distortion: harmonic distortion
An audio signal can be broken down in repetitive cycles. The speed at which these cycles repeat is called frequency. The length of a single cycle is called a period. Non-linear distortion adds to the output signal frequencies that were not originally present in the input signal. There can be both harmonic and non-harmonic frequencies added. A harmonic is a whole number multiple of the root frequency. For instance, the second harmonic of a G at 392Hz is 784Hz (392 × 2), the third harmonic is 1568Hz (392 × 3), etc. A musical sound (a periodical sound, that is) has a fundamental frequency (the main wavelength), which characterizes the pitch of he note, and harmonics (proportional wavelengths), which are not as predominant but nevertheless add a lot to the timbre of a sound.
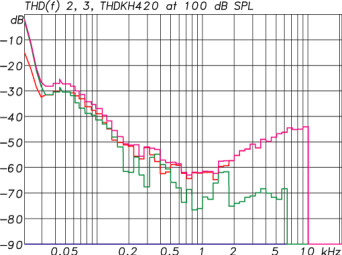
Using a pure wave (without harmonics, like a sine wave) as source signal, it’s easy to find the harmonic distortion present at the output. You then have to sweep the entire frequency range to get a set of contour lines (one per each harmonic measured). The Total Harmonic Distortion (THD) is indicated as a ratio between the level of the harmonics and that of the fundamental. It is expressed as a percentage or in dB, together with the overall volume at which the measurement was made, as well as a frequency range. For example: THD = 3% @ 90dB SPL (100 Hz – 20 kHz). It’s interesting to note that, in psychoacoustic terms, the sense of degradation of a signal isn’t proportional to the THD rate. For instance, the second harmonic in particular is often considered to add “roundness” to a sound.
On the image to the left you can see the THD curves of a Neumann KH420 speaker. In violet: total harmonic distortion. In red: second harmonic. In green: third harmonic. On the left side is the difference with the fundamental. At the bottom, the frequency. Since the second harmonic of 10kHz is 20kHz, the upper limit of human hearing range, the curve stops at 10kHz.
Non-linear distortion: intermodulation
Things get a bit more complicated when the signal source is made up of several notes played simultaneously, each with its own fundamental. In this case, besides harmonic distortion you also get intermodulation distortion (IMD), in other words, frequencies that aren’t whole-number multiples of the fundamental frequencies present. They have no musical correlation to the fundamental and, hence, significantly degrade the listening quality. The intermodulation distortion rate is never specified in the specs of loudspeakers (except for experimental purposes). Intermodulation varies so much depending on the source signal that the results aren’t very significant.
Generally speaking, speaker catalogs are pretty scanty when it comes to distortion measurements. They aren’t easy to make, the test signal to measure IMD isn’t standardized and, since speakers are the stage in the audio chain that add more distortion, manufacturers don’t seem to be too eager to shock their clients… The THD rate of a speaker can easily amount to 5%, and even more in the lower frequencies. In comparison, solid-state amps have a THD of < 0.1% across the entire frequency spectrum.