Last time I told you we would discover a couple of somewhat particular scales: the harmonic major and double harmonic major scales. But they belong to a larger group called synthetic scales, which I think we should discuss before we move into these two specific cases.

Enter synthetic scales
To really grasp the nature of synthetic scales, it’s important to understand that these scales are not taken directly form the circle of fifths (article 3) like traditional major scales, their relative minors and the natural modes that stem from them. Synthetic scales owe their name to the fact that they are either a hybrid between different modes or the specific modification of certain notes within specific modes. In fact, you already know two cases that imply note modifications: the “unnatural” minor modes, in other words, the harmonic and melodic minor modes. They are the result of the “artificial” swap of the minor seventh for a major seventh. But let’s not get ahead of ourselves. It’s confusing enough as it is, isn’t it? I sense I’m losing some of you, especially those of you at the back…! But it’s normal, don’t worry, I’ll try to bring some light into the matter.
The great return of tetrachords
To discuss the hybridization of modes, you first have to understand the rules it follows. For the sake of clarity, I’ll begin reminding you that hybridization is a term used in biology to designate the way species mix with each other. Yes, I know this is not why you got into music, but bear with me and follow me into music’s Island of Dr. Moreau. Okay, let’s not digress here…
This hybridization takes place by splitting in two the two modes you want to merge, to then combine them. Does this splitting sound familiar? Right, it’s the same splitting we started studying (although a bit frugally) in article 49, when I mentioned tetrachords.
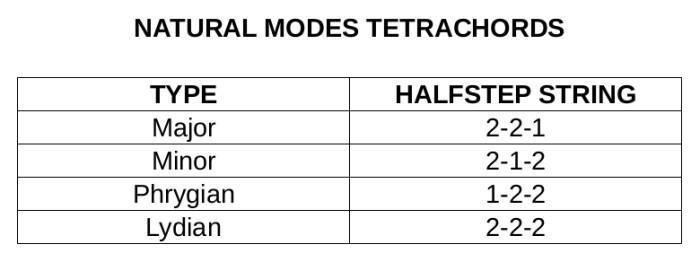
As a brief reminder: there are four types of tetrachords in the natural modes, which own their name to the main characteristics of the modes they belong to. Hence, each of them includes the characteristic note of the mode in question. The table below will allow you to easily find the names and construction of tetrachords. The construction is determined by the intervals that separate the notes of the tetrachord. Here’s an example for the C-D-E-F major tetrachord: the intervals are of two full steps between C and D, two semitones between D and E and, finally, one semitone between E and F, which results in the following series: 2–2–1.
In the coming articles you’ll see how and why you can combine different tetrachords, how the tetrachords from altered modes are built, and how synthetic scales are formed not by hybridization but by note modification.