In the previous article you learned that FM synthesis allows the creation of harmonically rich sounds. Today we'll see what that means in terms of frequency spectrum....
Of math and frequencies
The harmonic spectrum depends on the relation between the carrier © and the modulating (M) signals. If C/M is an integer, the frequencies produced will be harmonics of the two frequencies C and M. If C/M is not an integer, the spectrum will be inharmonic. Composer Barry Truax (see previous article) classified the different C/M relations produced by FM synthesis in different sound families, to facilitate their use.
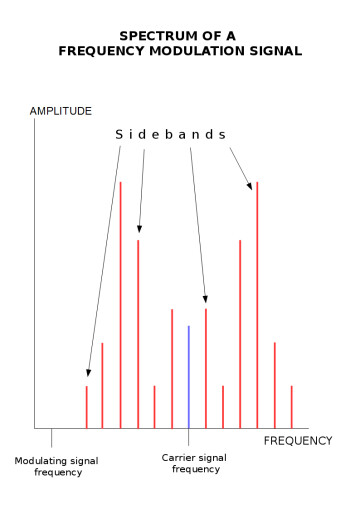
Besides the nature of the harmonic spectrum of the signal, there’s also the question of bandwidth. As a reminder, the bandwidth of a signal represents all the frequencies it comprises. Within the frame of FM synthesis, the bandwidth depends entirely on what is called the modulation index (I). This index is given by the formula I=D/M, where D stands for the quantity of frequency deviation or depth applied to the carrier, and M is the frequency of the modulating waveform. To put it simply, the modulation index expresses the amount of modulation experienced by the carrier.
Finally, the amplitude of each frequency within the signal is determined by a mathematical function, called “Bessel function.” Without going into math details that fall outside the scope of this article, you could simply say that ─ within the frame of FM synthesis ─ this function, which integrates the modulation index in the equation, results in very interesting behaviors of the audio signal. The first one being that the maximum amplitude and power of the signal do not vary with the modulation index. In other words, you can vary the modulation index as much as you want, but it will not affect the signal’s overall volume. The other main characteristic of a signal created with FM synthesis is that, the more you increase the modulation index, the more the frequency amplitude of C diminishes, in relation to the overall signal, in favor of the sidebands. It can even disappear completely, which makes FM synthesis resemble ring modulation (see article 14), but with a much larger number of sidebands.
FM synthesis ─ When and where?
As you already saw, while FM synthesis isn’t unimaginable in the analog world ─ John Chowning, its “discoverer, ” was actually the first to compose a work exclusively based on analog FM synthesis, back in 1966 ─ it’s in the digital realm where it’s really thrived. And it was none other than Chowning himself the first to experiment with the digital implementation of his discovery.. After patenting his work in the early '70s, he vainly tried to interest American companies in his research, but it was finally Yamaha who was attracted it.
The Japanese company developed and improved Chowning’s principles and introduced the GS 1 digital synthesizer in 1980, and, most notably, the DX7 in 1983. The latter became a worldwide success due to its relatively affordable price for the time (about $2000), its exceptional stability, resulting from its digital nature, and the completely different sounds it offered. It was used on countless productions by superstars of the likes of Phil Collins, Michael Jackson and Madonna. Yamaha went on to create an entire series based on it, comprising half a dozen models, the most celebrated of which was the DX7–2.
Native Instruments later emulated the DX7 in software, with the FM7, which would become the FM8 in 2006. There’s even an open-source emulation called DEXED.
My geeky side can’t refrain from mentioning yet another field of application of FM synthesis, namely the first Adlib and Sound Blaster soundcards! Indeed, the harmonic richness of the signals produced with FM synthesis is (or at least it was, back then) ideal to create all sorts of sound effects for video games.
Not to mention that it allowed some of us ─ including yours truly, on a basic but endearing Amstrad PC 1512 ─ to discover a different type of computer music that broke free from the tyranny of the Ataris and Amigas!
Conclusion
FM synthesis rose to stardom due to the possibilities it offers to create extremely rich sounds with a reduced number of oscillators/operators, while at the same time being an alluring alternative to the resource-intensive additive synthesis.
Yet, the computing power of digital hardware has increased so much that additive synthesis has become much more simpler to produce than in the past, not to mention granular synthesis or physical modeling synthesis, which we will study in upcoming articles.
What’s more, FM synthesis is well-known for being intuitive and for producing very different results with tiny parameter modifications. That’s one of the reasons (together with the great number of parameters that need to be controlled) why FM synthesis was implemented very little in analog systems: Analog oscillators (VCOs, see article 6 of this series) aren’t stable enough for this type of synthesis, as they’re capable of going berserk with even the slightest frequency variation of one of the oscillators. But that’s also what makes it so appealing in the eyes of many people, like yourself, don’t deny it!
Finally, remember that FM synthesis doesn’t concern dedicated instruments only, like the DX7, but also any analog synth whose oscillator output can be routed to the CV input of another one… Food for thought… more on this in the next article!