In the fifteenth article of this series, I briefly mentioned FM while introducing the different forms of synthesis. Now, the time has finally come to discuss it, but before we do that I must first talk a bit about...
Amplitude modulation or AM synthesis
In the fourteenth article we already saw ring modulation, and in the last two articles we saw how an envelope can be applied to a waveform (to create grains, remember?). Well, these two principles are directly related to amplitude modulation, too.
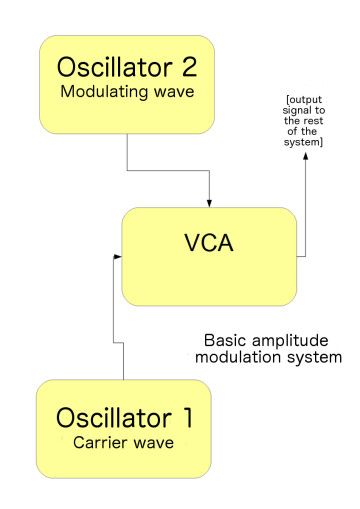
One of the points in common with ring modulation is that you have a carrier signal © whose amplitude is modulated by a modulating signal (M). The difference resides in the fact that, in ring modulation, the M waveform is “bipolar, ” meaning it oscillates from positive to negative values (above and below zero).
In amplitude modulation, however, the modulating signal is “unipolar, ” which means it only exists in the positive domain. And that’s how amplitude modulation relates to the principle of an envelope applied to another signal, in this case, an envelope that evolves only between 0 and 1. As long as the modulating signal M isn’t within the audible range — meaning it doesn’t exceed 20 Hz — it acts as an envelope on the carrier signal. The result is a sort of tremolo, as described in article 13 of this series.
However, when the frequency of M enters the audible range, it comes upon C to generate frequency sidebands, as with ring modulation (see article 14), which constitutes their second point in common. But there is a difference: While a ring modulator makes the frequency of the carrier wave disappear, it’s kept along with the sidebands in amplitude modulation.
Of frequency modulation, vibrato and radio
Okay, no more beating around the bush, after this brief, but necessary detour to describe amplitude modulation, we can finally address frequency modulation, also known as FM.
Just like amplitude modulation, FM synthesis is based on the principle of a carrier wave being modulated by a modulating wave. With the difference that this time around, the modulating signal doesn’t act on the amplitude of the carrier, but rather on its frequency.
While amplitude modulation recalled the tremolo effect, with FM it’s the vibrato effect (also mentioned in the thirteenth article of this series) that comes to mind. In fact, FM synthesis could be considered an extreme form of this effect. And it was actually playing around with vibrato that Stanford’s John Chowning realized, back in the 1960s, that beyond a certain point, the vibrato effect disappeared to give way to the emergence of a complex harmonic signal. And, thus, FM synthesis was born!
Are you wondering what’s the difference with FM radio? It’s pretty simple: The only difference is that in FM radio the carrier can’t be heard because it’s in the frequency range from 87.5 MHz to 108 MHz. Let’s see now how all this works.
Operators
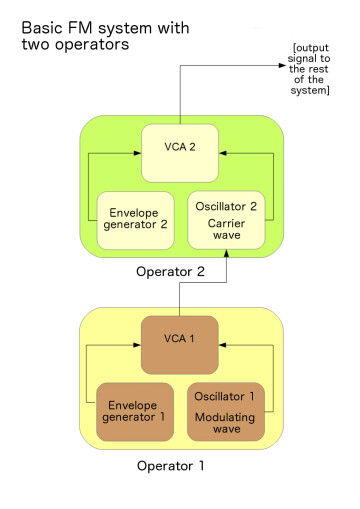
FM synthesis doesn’t rely solely on the use of oscillators, but rather on so-called operators. An operator is the combination of a sine wave oscillator, a VCA/DCA and an envelope generator (for more on these concepts, refer to article 8).
The number of operators is unlimited. Operators can either modulate each other in terms of frequency, or their signals can be simply summed. This second approach goes beyond frequency modulation and is somewhat closer to additive synthesis!
Operators can also use their own signal as a modulating wave. This can result in very rich signals, but it can also result in a periodic sound being easily transformed into noise (see article 5).
And now, let’s see how the frequencies present in the signal behave.
Frequencies, anyone?
I’m talking about a complex signal, and rightly so! In fact, there isn’t a limit of two sidebands in FM like there is in AM synthesis. In theory, there’s no limit. This makes FM synthesis particularly interesting: With only two oscillators…sorry, operators!… you can get a signal that is extremely rich in harmonics. But it’s still far from additive synthesis, which would require a considerably larger number of oscillators (one per frequency element). By the way, FM synthesis forms part of a big family, called “animated spectrum” synthesis, which includes all forms of synthesis that produce a signal whose frequency content doesn’t require a filter to evolve (like the FM, AM and granular synthesis we’ve seen here).
You could also say that FM synthesis is very similar to phase modulation, the only difference between them being the amplitude of the overtones (see next paragraph) they generate.
Each sideband corresponds to the carrier’s frequency plus or minus an integer multiple of the modulating frequency. Theoretically, this integer can be any value, which would result in an infinite number of frequency values, something that is obviously impossible in the real world. But you’ll have to wait until the next article to learn more about that…!