Some people might think it's weird to see sampling considered as a type of synthesis. Indeed, throughout this series of articles, I've been telling you all the time about the creation of sounds "from nothing" and, all of a sudden, the playback of pre-existing sounds pops up out of nowhere!
What’s that all about, you ask? As we saw in the previous article, it’s important to note that this path was taken by some manufacturers due to the complexity of additive synthesis, and that sampling can be considered as a natural evolution in the search for new sound-creation forms. We should also add that sampling is only the basis for the production of sound: Sampled sounds can the be processed by filters, envelopes, LFOs, etc., like any waveform produced by an oscillator. Sampling has been revolutionizing the way music has been made over the last couple of decades, be it with wavetable synthesis or the introduction of hardware and software samplers.
But let’s start by defining what sampling is, even if it diverts us a bit from sound synthesis in itself.
Sampling
Sampling is the digital recording of an analog signal by means of an analog-to-digital (ADC or A/D) converter. But why is that called sampling? Because, unlike an analog recording (on a magnetic tape, for example), which records a continuous signal, the digital recording takes only samples of the signal at regular intervals.
Take, for instance, a digital recording on a CD, which uses a sampling rate of 44.1 kHz with a 16-bit resolution. This means that the system will “copy” 44,100 samples per second of the original signal and that each of those samples will be coded by a binary number with 16 positions. A smoothing filter is then used to make the reproduction of each sample, one after the other, more coherent.
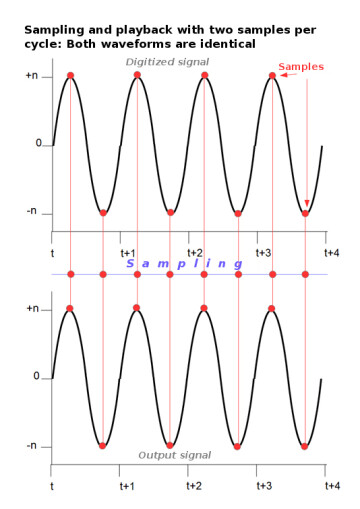
This number, 44.1 kHz, was chosen for the following reason: It was proven that you need at least two samples per cycle of any given waveform (see articles 2 and 3 of this series for info on waveforms and their cycles) for it to be reproduced correctly by the playback system and the digital-to-analog (DAC or D/A) converter.
If you consider that, in theory, the upper limit of human hearing is 20 kHz, you need a sampling rate of at least 40 kHz to capture and reproduce the human hearing range correctly. And since some people can hear beyond that limit – Rudolph Koenig, a German engineer originally responsible for international acoustic standards, was said to be able to hear up to 23 kHz – it was decided to extend it to 22 kHz.
But that’s not the only reason.
Nyquist frequency and aliasing
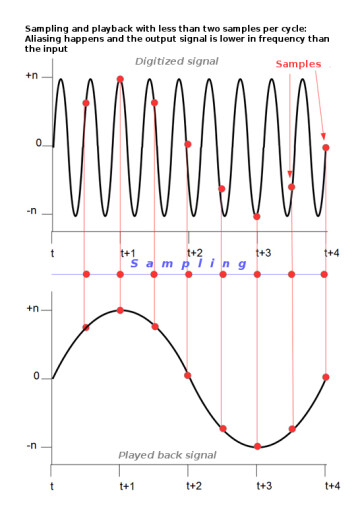
The frequency that is exactly half the maximum sampling frequency is called the Nyquist frequency. Sounds that exceed this frequency during a digital recording are reproduced during playback in the lower frequencies. Thus, they “corrupt” the signal. This phenomenon is called aliasing.
Here’s an example: The third harmonic of a 12.5 kHz signal is 37.5 kHz, which, in theory, can’t be heard by human beings. The problem is that due to aliasing with a 44.1 kHz system, it turns into (44.1 – 37.5) = 6.6 kHz, which is perfectly audible… and annoying. This means you’d need a system working at (37.5 × 2) = 75 kHz for this frequency not to be shifted down into the audible range.
That’s why anti-aliasing filters are used during recording to remove frequencies above the Nyquist frequency.
In certain cases, you can only use sine waves above 11.025 kHz in sound synthesis, in order to avoid any harmonics that could potentially produce aliasing.
Anyway, in the next article we’ll take a closer look at sampling and its different applications.